I think another thing to consider with time constants and filters is that a time constant represents when phase shifts occur. In FerdinandII's example he used the RIAA response: I don't have that circuit simulated but I have an inverse RIAA circuit used to test pre-amps.
Attachment:
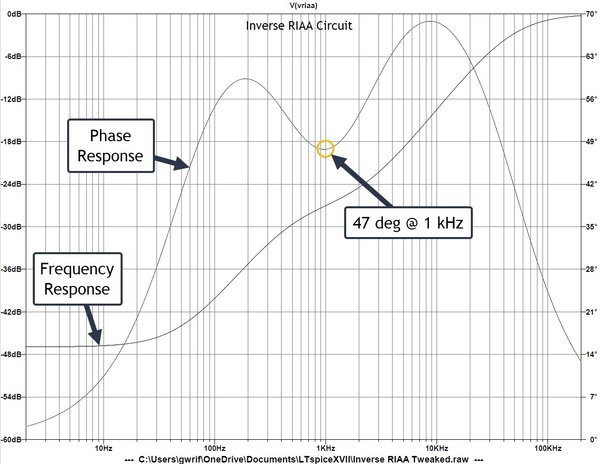 Inverse RIAA Response.jpg [ 164.84 KiB | Viewed 81692 times ]
Inverse RIAA Response.jpg [ 164.84 KiB | Viewed 81692 times ]
The one line shows the frequency response with respect to the left axis and the other line shows the associated signal-phase shift with respect to the right axis. Note that the output signal from this circuit is shifted by 47 deg at 1 kHz. This represents a time shift of about 130 usec and a sound-wave shift of 48 mm (ahead of the input signal, if I remember right.) Likewise, this output is shifted 10 deg at 10 Hz, 68 deg at 10 kHz, and 13 deg at 200 kHz.
(Please, someone correct me if this is wrong: I don't want to muddy the water!)

The importance makes more sense to me in speakers. 1 kHz has a wavelength of 0.343 m in air at 20 deg C. The phase shift of 47 deg makes the sound wave appear 48 mm earlier than the speaker signal (almost 2 inches,) which will cause problems with sound stage and imaging in a two- or three-way speaker system.
I think that this is why time constants are important to keep track of. As dberning said, there are numerous RC, LC, RL, and LRC time constants in our circuits and if we can select the time constants to minimize phase shift, then we should have a system with better imaging and sound stage.
Or am I wrong?




